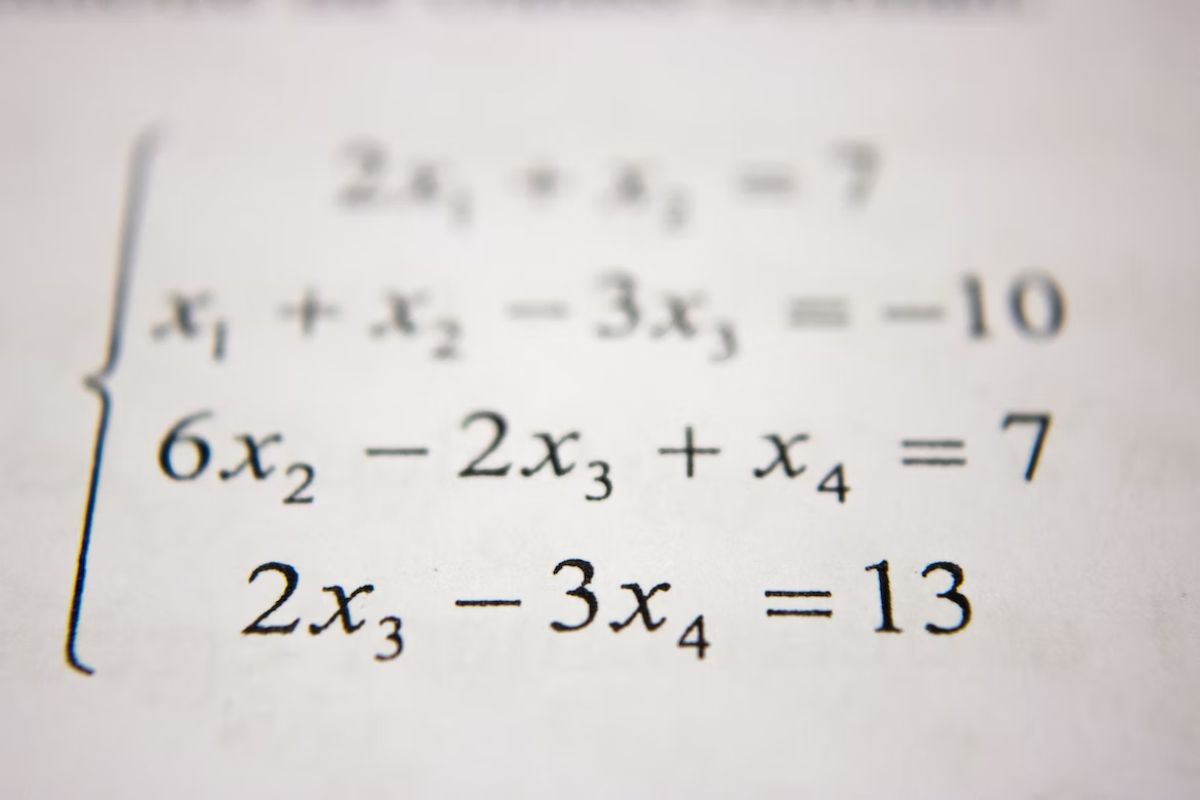Persamaan linear terdiri dari suku yang mengandung konstanta. Lalu, bisa juga disebut perkalian konstanta dengan variabel tunggal. Sebenarnya, kamu sudah pernah mempelajarinya saat masih kelas VIII.
Lalu, mengapa disebut dengan linear? Sebab, hubungan ini dideskripsikan dengan garis lurus dalam sistem koordinat kartesius. Selain itu, persamaan ini juga memiliki lawan, yakni pertidaksamaan linear.
Pada kesempatan ini, kamu akan belajar lebih dalam mengenai persamaan linear matriks dan lainnya di bawah ini.
Pengertian Persamaan Linear

Mengutip buku berjudul Mengenal POM QM karya Sandi Ragil Putra, sistem ini merupakan persamaan aljabar. Persamaan tersebut juga memiliki karakteristik, di mana setiap sukunya mengandung konstanta.
Lalu, persamaan ini juga disebut dengan hubungan matematis. Sebab, sistemnya menetapkan setiap titik secara unik. Kemudian, ada di dalam bidang dengan rangkaian koordinat numerik. Ada dua sifat utama dalam sistem persamaan ini, yaitu:
Contohnya, l merupakan persamaan dari linear. Jadi, sifatnya adalah sebagai berikut:
- Penambahan dan pengurangan bilangan dalam kedua persamaan l, tidak mengubah solusi persamaannya.
- Lalu, perkalian bilangan tidak nol pada kedua persamaan l, juga tidak mengubah solusi persamaannya.
Supaya kamu bisa memahaminya, maka persamaan ini terbagi menjadi tiga jenis. Hal itu disesuaikan dengan jumlah variabelnya. Berikut adalah jenis-jenis persamaan dari linear.
Sistem dan Jenis Persamaan Linear

Jika kamu menemukan lebih dari satu persamaan linear serentak dan lainnya, maka hal tersebut akan menjadi sebuah sistem. Jadi, bentuk umum dari persamaan linear adalah sebagai berikut:
y = mx + b
Selain itu, ada pula berbagai persamaan lainnya dari linear, yakni:
1. Satu Variabel
Sistem ini hanya memiliki satu variabel atau berpangkat satu. Bentuk umumnya adalah ax + b = o. Jadi, a dan b adalah bilangan bulat. Lalu, bukanlah o dan b secara konstanta.
2. Dua Variabel
Sistem ini mengandung persamaan dua variabel berpangkat satu (x dan y). Kemudian, tidak mengandung perkalian di antara kedua variabel (suku xy). Bentuk umum dari persamaan dua variabel adalah ax + by = c. Lalu, a, b, dan c merupakan konstanta dari bilangan real.
3. Tiga Variabel
Persamaan tersebut mengandung tiga variabel. Secara umum, kamu bisa menulis bentuknya dengan ax + by + cz = d. Untuk menyelesaikannya, kamu harus menemukan pasangan bilangan x, y, dan z.. Untuk menyelesaikan persamaan linear x y z, maka bisa menggunakan metode substitusi.
Unsur Persamaan dari Linear

Terdapat beberapa unsur persamaan dari linear, yaitu:
- Variabel: pengganti bilangan yang nilainya belum diketahui. Umumnya, variabel digambarkan dengan huruf a, b, c, d, hingga seterusnya.
- Koefisien: bilangan ini menjelaskan banyaknya jumlah dari variabel sejenis. Jadi, letak koefisien berada di depan variabel.
- Konstanta: nilai bilangannya konstan. Sebab, tidak diikuti dengan variabel di belakangnya.
- Suku: bagian dari bentuk persamaan yang meliputi koefisien, konstanta, dan variabel.
Selanjutnya, kamu perlu mengetahui metode penyelesaian dari persamaan ini. Simak penjelasannya di bawah ini.
Metode Penyelesaian Linear
Kamu bisa menggunakan beberapa metode ini untuk menyelesaikan soal persamaan linear, yakni:
- Grafik: menentukan grafik garis dari masing-masing persamaan. Lalu, menentukan titik potong dari kedua garisnya.
- Eliminasi: menghilangkan salah satu variabel yang ada di dalam persamaan. Jika ditemukan persamaan a dan b, maka kamu harus mencari nilai a. Kemudian, kamu juga harus menghilangkan b terlebih dahulu.
- Substitusi: mengubah satu variabel dengan variabel dari persamaan lain.
- Eliminasi-Substitusi: penggabungan dari metode eliminasi dan substitusi. Pertama, kamu bisa mengeliminasi salah satu variabelnya. Kemudian, variabel yang didapatkan harus disubstitusikan dari salah satu persamaan.
Selain itu, persamaan ini juga memiliki ciri-ciri. Berikut adalah ciri-ciri dari linear:
- Memiliki pangkat satu.
- Tidak adanya perkalian variabel.
- Terdiri dari dua ruas yang dikaitkan melalui tanda sama dengan (=).
- Penambahan, pengurangan, pembagian, hingga perkalian di keduanya tidak bisa mengubah nilai persamaannya.
Jadi, sekian penjelasan mengenai persamaan linear beserta metodenya. Kamu harus terus belajar dan berlatih agar memahami persamaan ini. Lalu, pastikan juga kamu mencari contoh soal untuk dijadikan sebagai bahan latihan. Dengan begitu, kamu bisa menguasai persamaan ini dengan mudah.