Pertidaksamaan nilai mutlak adalah pertidaksamaan dengan nilai yang benar untuk setiap nilai pengganti variabelnya. Sedangkan pertidaksamaan palsu merupakan pertidaksamaan dengan nilai selalu salah untuk tiap pengganti variabelnya.
Pertidaksamaan sendiri merupakan materi Matematika yang sifatnya terbuka dan memuat berbagai ungkapan seperti >, ≥, <, atau ≤. Nilai mutlak dikenal juga dengan sebutan absolut yang artinya bisa dipastikan benar.
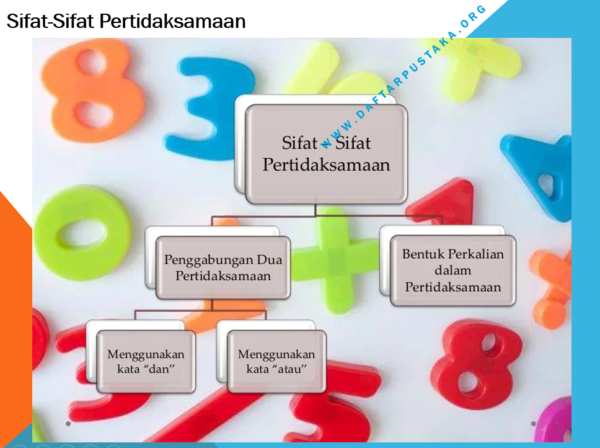
Sifat-Sifat Pertidaksamaan
1. Pertidaksamaan Kuadrat
Pertidaksamaan kuadrat merupakan pernyataan dalam Matematika yang menghubungkan ekspresi kuadrat sebagai kurang dari atau lebih besar dibandingkan dengan yang lainnya. Menghitung pertidaksamaan kuadrat sebenarnya tidak terlalu sulit dan bisa dikerjakan dengan mudah jika mengetahui caranya.
Untuk menyelesaikan pertidaksamaan kuadrat, pertama harus ditentukan terlebih dahulu bagian mana dari grafik fungsi kuadrat yang terletak di bawah atau di atas sumbu x. Nilai tersebut bisa dicari dengan menggunakan grafik atau secara aljabar dengan bentuk umum sebagai berikut:
ax2+bx+c>0. ax2+bx+c≥0.
2. Pertidaksamaan Tingkat Tinggi
Pertidaksamaan tingkat tinggi adalah pertidaksamaan yang memiliki derajat lebih dari 2. Hal tersebut dijadikan sebagai bentuk penghubung antara ruas kiri dan kanan, sama seperti pada pertidaksamaan linear dan pertidaksamaan kuadrat.
Beberapa penghubung yang umumnya digunakan adalah kurang dari sama dengan (≤), lebih dari sama dengan (≥), lebih dari (>), dan kurang dari (<). Berikut beberapa langkah penyelesaian pertidaksamaan jenis ini:
- Sama dengan pertidaksamaan kuadrat, penyelesaian pertidaksamaan ini dilakukan dengan cara memindahkan semua suku ke dalam satu ruas, misalnya sebelah kiri sehingga tidak ada lagi yang tersisa atau bernilai 0 pada ruas kanan.
- Faktorkan suku yang sudah dipindahkan ke dalam bentuk derajat yang lebih rendah. Hal tersebut dilakukan untuk menemukan nilai
- Jika nilainya sudah diketahui, susunlah pada garis bilangan. Sama dengan bentuk garis bilangan pada umumnya, Anda harus menentukan tanda (-) atau (+) pada area masing-masing.
3. Pertidaksamaan Pecahan
Jenis pertidaksamaan yang satu ini merupakan pertidaksamaan dengan fungsi yang dijabarkan dalam bentuk pecahan yang memiliki penyebut dan juga pembilang. Cara penyelesaiannya sebagai berikut:
- Ruas sebelah kanan harus dijadikan 0 terlebih dahulu.
- Samakan semua penyebut yang ada di ruas sebelah kiri.
- Faktorkan pembilang dan penyebutnya
- Carilah nilai dari setiap variabel yang menyebabkan pembilang dan penyebut bernilai sama dengan nol.
- Gambar sebuah garis bilangan yang berisi semua nilai yang telah didapatkan.
- Apapun tanda yang ada pada pertidaksamaannya, nilai 0 untuk penyebut selalu digambar dengan titik putih (penyebut sebuah pecahan tidak boleh sama dengan 0 agar memiliki nilai.
- Tentukan tanda (-) atau (+) pada masing-masing interval.
4. Pertidaksamaan Irasional / Pertidaksamaan Bentuk Akar
Pertidaksamaan jenis ini memiliki ciri khas yang berbeda dengan bentuk yang lainnya, yaitu variabelnya yang terdapat di dalam tanda akar. Berikut cara penyelesaiannya:
- Jadikan bagian ruas kanan sama nilainya dengan 0 (nol).
- Kuadratkan kedua bagian ruas.
- Selesaikan dengan menggunakan cara yang sama seperti pertidaksamaan kuadrat atau linear, dengan syarat nilai yang berada dalam setiap tanda akar harus ≥ 0.
Pertidaksamaan Nilai Mutlak
Sama dengan persamaan mutlak, sebuah soal yang terkait dengan pertidaksamaan nilai mutlak biasanya mengharuskan Anda untuk mencari himpunan penyelesaian yang pertidaksamaan tersebut.
Namun, harus diperhatikan bahwa dalam perhitungan soal pertidaksamaan harus dilakukan secara teliti dan membagi kedua ruas, sama seperti mengerjakan soal persamaan karena tanda dari pembagi yang bernilai (+) atau (-) dapat membuat tanda dari sebuah pertidaksamaan jadi berkebalikan.
Pertidaksamaan memiliki tanda penghubung untuk memisahkan ruas kanan dan kiri. Beberapa jenis penghubung yang digunakan adalah lebih dari (>), lebih dari atau sama dengan (≥), kurang dari (<), dan kurang dari atau sama dengan (≤).
Pertidaksamaan nilai ini adalah pertidaksamaan yang variabelnya terdapat dalam tanda mutlak. Soal pertidaksamaan bisa diselesaikan dengan menggunakan konsep yang dimiliki oleh sifat persamaan nilai mutlak.
Pertidaksamaan dengan Harga Mutlak
1. Pertidaksamaan
Pertidaksamaan merupakan kalimat dalam Matematika terbuka yang berisi ungkapan ≤, ≥, >, atau <. Sedangkan pertidaksamaan harga mutlak merupakan pertidaksamaan yang memiliki nilai selalu benar pada setiap pengganti dalam variabelnya.
2. Sifat-Sifat Pertidaksamaan
Menemukan nilai mutlak tidaklah mudah, Anda harus mengikuti 2 aturan utamanya. Nilainya akan positif jika fungsi yang terdapat dalam tanda mutlak lebih dari 0 dan akan bernilai negatif jika fungsi tersebut kurang dari 0.
Dalam pertidaksamaan harga mutlak terdapat pertidaksamaan aljabar yang ekuivalen dengan hal tersebut dan disebut sebagai sifatnya.
Sifat tersebut digunakan untuk dapat menentukan himpunan penyelesaian dari soal pertidaksamaan yang diberikan. Untuk lebih jelasnya, simak beberapa sifat dari pertidaksamaan harga mutlak sebagai berikut:
3. Pertidaksamaan Harga Mutlak
Pertidaksamaan harga mutlak memuat variabel yang memiliki tanda mutlak. Pertidaksamaan ini memiliki nilai yang selalu benar pada bagian setiap nilai pengganti variabelnya. Pertidaksamaan ini sering juga disebut dengan ketidaksamaan yang termasuk dalam kalimat bagian Matematika tertutup.
Baca Juga :
- Sejarah Demokrasi Terpimpin, Fase Suram Demokrasi di Indonesia
- Peta persebaran Flora dan Fauna di Indonesia
Contoh Soal Pertidaksamaan Nilai Mutlak
Agar bisa memahami materi pertidaksamaan nilai mutlak, Anda harus mempelajari contoh soal dan pembahasannya terlebih dahulu. Contoh soal bisa dijadikan sebagai sarana latihan agar Anda bisa menyelesaikan soal terkait dengan lebih mudah dan cepat. Simak contohnya sebagai berikut:
- Selesaikan soal tentang himpunan pertidaksamaan nilai mutlak sebagai berikut!
|5x+10|≥20
Penyelesaian Soal Pertidaksamaan Nilai Mutlak
Untuk dapat menyelesaikan soal diatas, digunakan sifat pertidaksamaan nilai mutlak sebagai berikut:
Jika a>0 dan |x|≥a
Maka x≥a atau x≤-a
Sehingga bisa kita tulis:
5x+10≥20
5x≥10
x≥2
5x+10≤-20
5x≤-30
x≤-6
Maka himpunan penyelesaiannya adalah: x≥2 atau x≤-6

Dengan adanya contoh pertidaksamaan nilai mutlak Anda bisa mempelajari materi ini secara lebih dalam. Lakukan latihan secara rutin agar bisa menyelesaikan berbagai soal terkait materi tersebut dengan lebih cepat dan tepat.






